Wave-like Behavior Probability

2024-10-0214:59 Status:CHEM121 Tags: Quantum mechanics

In a Chemical Context

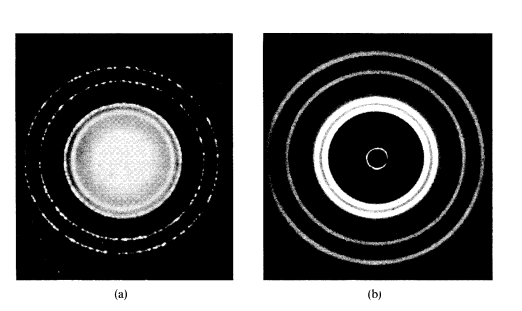
Recall: Diffraction, and interference in Simple Harmonic Motion (SHM). In Rutherford’s Gold foil experiment electrons passed through the foil in concentric circles. This would suggest that electrons can interfere constructively and destructively as waves do.

If particles can behave as waves there must be some expression that relates the particle’s momentum (a characteristic quality that defines a particle in the classical sense) to its wavelength (a characteristic that all waves have). The de Broglie equation relates the two:

$\lambda =\frac{h}{p}=\frac{h}{mv}$ Where $\lambda$ is the wavelength in $m$, $p$ is the momentum, $h$ is Planck’s constant $6.626\times 10^{-34}Js$, $m$ is the mass of the particle in $kg$, and $v$ is the velocity of the particle in $m/s$.

Planck’s constant explains why tennis balls don’t spontaneously split into two, or why footballs have a visible wavelength. However, for particles where the mass is very small, a wavelength can be observed. Recall transverse waves and their form:

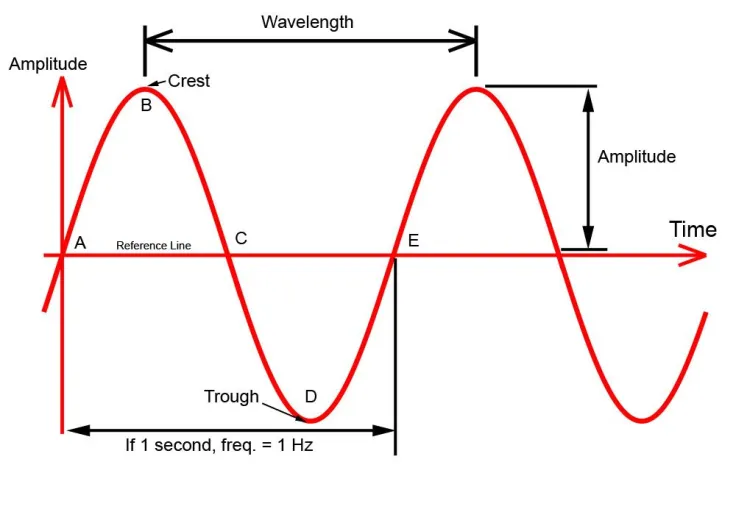
Sine waves: many wave phenomena in nature, including electromagnetic radiation (light), and de Brogolie waves, can be represented by the sine mathematical function, which is a smooth repetitive oscillation. $f(x)=A\sin (\frac{2\pi x}{\lambda })v=f\lambda$ Where $A$ is the constant (an amplitude), $x$ is the distance from the origin, $\lambda$ is the wavelength. And for the equation describing the speed of the wave, $f$ is the frequency (also represented by $\nu$) Note that $f(x)$ is unitless. It is also useful to know that the speed of light is $3.0\times 10^{8}m/s$. In order to capture a wave, boundaries are imposed to restrict the movement of the wave/make it more predictable:

Mathematically, standing waves extend from $-\infty$ to $+\infty$ thus causing the property of waves to occupy the size of its container. For example, a water wave can occupy an entire swimming pool. For such a wave, can we say if it is at the beginning of the pool, at the middle or at the end? No. The wave exists simultaneously everywhere. If a quantum particle is represented by a wave, then where is the particle? According to quantum mechanics, a quantum particle, like a water wave, exists simultaneously everywhere. However, if the wave only exists within a finite “1-D box,” then more information about the particle’s position/speed can be found.

Recall standing waves: They are waves bound on both ends, and have a length $L$ They have nodes where the amplitude of the wave is always 0. For more see Standing waves. These waves predict the likelihood that a particle will be at a certain position at a certain point in time. Unlike classical particles (such as tennis balls), waves are located everywhere and cannot be predicted with the same certainty. This is known as Heisenberg’s Uncertainty Principle:

One cannot know precisely (with zero uncertainty) both the position and momentum of a microscopic particle at the same time

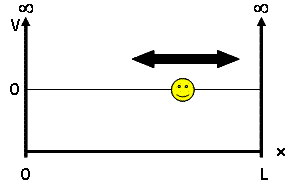
• Note that the length of the box has a length $L$.

If the energy is conserved in the 1-D box, then the particle will move at constant speed. The total energy of the particle in the box is: $E=\frac{1}{2}m{v}^2=\frac{p^2}{2m}$ Where the momentum, $p$ is related to the particle’s mass, $m$ and its velocity, $v$ by the classical equation, $p=mv$. When the particle is at rest, its velocity, momentum and kinetic energy would all be equal to zero.

If this classical particle were to be found in this box, then it would have a 100% chance of being found in the box (1):

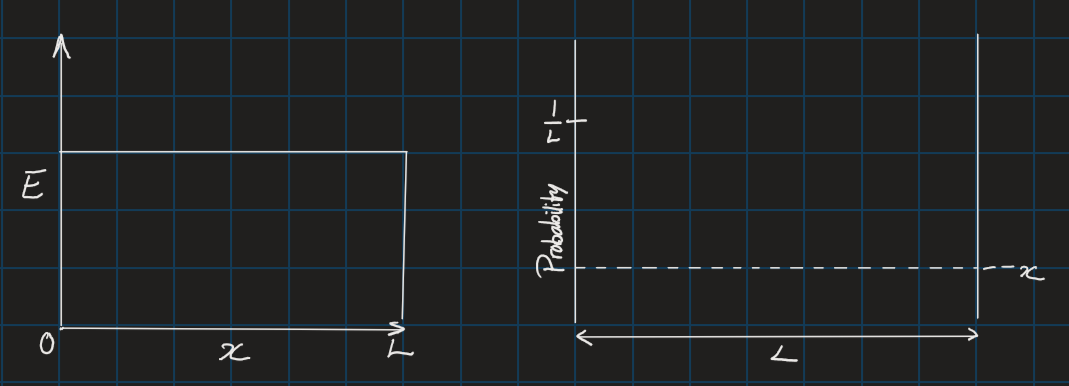
For a classical particle, the probability of finding it at any position $x$ is uniform. However, for electrons, and other small particles, the distribution is not uniform. This is where the Basics of quantum mechanics are applied to describe the wave functions for the distribution of finding smaller particles in a confined length, $L$

Quantum 1D Particle in a Box

Energy quantization: $E_n=\frac{h^2{n}^n}{8m{L}^2}$ The energy of the particle is quantized (can only be at certain values depending on $n$). The principle quantum number labels the state the particle is in…

…

$\Delta E=E_{final}-E_{initial}=\frac{h^2{n}_i^2}{8m{L}^2}-\frac{h^2{n}_f^2}{8m{L}^2}=\frac{h^2}{8m{L}^2}\cdot (n_f^2-n_i^2)$ If $\Delta E>0$ then the system absorbs energy If $\Delta E<0$ then the system emits energy

Source(s)