2024-10-2311:14 Status:PHYS106 Tags: Frame of reference & principle of relativity
Electromagnetism and Relativity
According to Maxwell’s equations for electromagnetism, light can be understood as a particular oscillation of electric and magnetic fields. These oscillations can travel as a wave through empty space, and the equations predict that such a wave has a speed of regardless of the direction its moving.
For ordinary scenarios, according to the principle of relativity, all three scenarios measure the same speed of light:
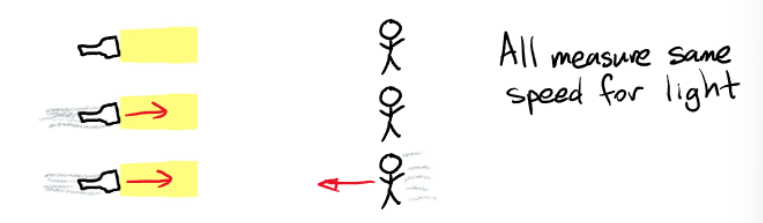
However, when objects move near the speed of light, time dilation and length contraction occurs.
Time Dilation
When observers in one frame of reference observe the physics in another frame of reference moving relative to them, they see time pass more slowly in the moving frame of reference. A simple argument shows why this is true:
Let be the time measured for light in an inertial frame to travel to the other end of a time clock (given that , and the height of the clock is
Let be the time for the light to reach the other side of the clock in a referential frame of reference. Where the clock moves at and the light travels at
Given both of these expressions, time Pythagoras’ theorem can be used to solve for the time dilation, .
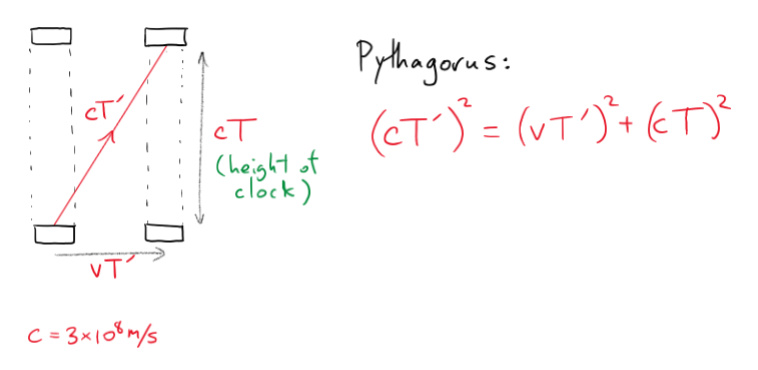 Solving for , (for comparable speeds to light)
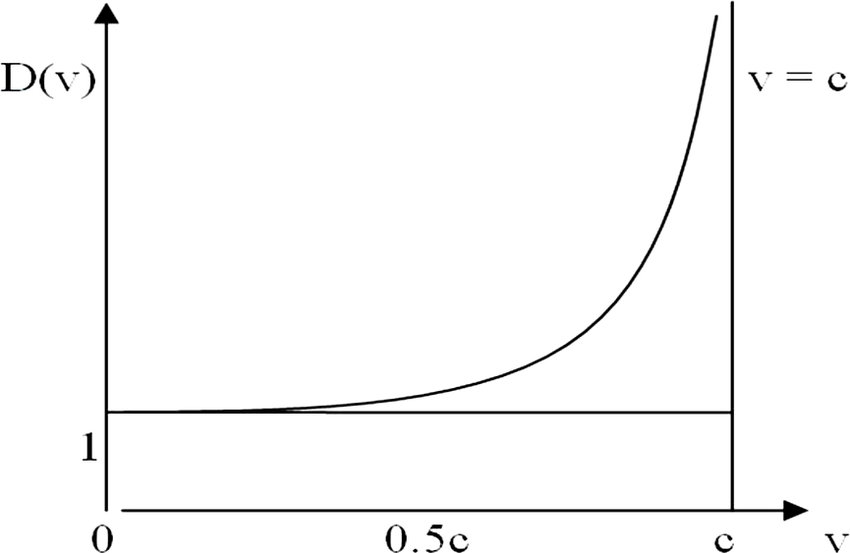
Note that always greater than 1. And dilated time will be more than time observed while moving at constant velocity. Generally, the other observed time will be passing “slower.”
Solving for , (for comparable speeds to light)
Note that always greater than 1. And dilated time will be more than time observed while moving at constant velocity. Generally, the other observed time will be passing “slower.”
A common question is: suppose there are a pair of twins and one twin goes on a trip at a large velocity and returns. According to time dilation, this twin will be younger than the other when she returns. But from the point of view of this twin, the other twin was the one moving and coming back, so shouldn’t they observe the other twin to be younger? The answer is no, because this first twin did not remain in an inertial reference frame the whole time. Our time dilation result applies to observers in a fixed inertial reference frame this travelling twin did not remain in a single reference frame for their journey. (They accelerate and decelerate to and from Earth’s surface so they are not in an inertial frame)
To observe the effects of this better, accelerating smaller particles to high speeds will allow for this dilation to be experimentally, and easily observed. Taking an unstable particle such as a muon (heavy electron) that has a predictable distribution of decay (half-life distribution), then it acts as a kind of clock.
Implications
- For very small values of , goes to 1, most kinematics and momentum formulas stay the same.
- As the clock is observed to run slowly, we can equivalently say that less time has passed for the moving clock than the stationary clock.
- If there are two perfectly synchronized clocks and take one of them on a trip with high velocity, when it returns to the starting point, it will read an earlier time.
Example
Muons are unstable elementary particles with a half-life of approximately . If a muon is produced in the upper atmosphere travelling at speed , how far would the particle be expected to travel before decaying?
\begin{gather} T' = T \cdot \frac 1 {\sqrt{1-\frac {v^2}{c^2}}} \\ T' = T \cdot \frac 1 {\sqrt{1-\frac {4^2}{5^2}}} \\ T' = 2\times 10^{-6} m/s \cdot\frac 5 3 \\ T' = 800m \end{gather}$$ ### Length Contractions Because objects are moving at different speeds, there is a contraction of length: Objects moving relative to observer are measured to be shorter than their actual length in direction of motion: $$D_{moving} = \frac {D_{actual\ (proper)}} \gamma$$ # Next: [[Relativity of simultaneity]]