2024-09-0412:53 Status: Tags:
Overview:
Broadly how does a function behave as a certain value is approached.
Definitions:
Power Law: A power law is an expression of the form (as a function of ), where we call the index: E.g. etc. Exponential: An exponential is an expression of the form (as a function of ), where and is known as the base. E.g. etc.
Power Law:
As functions get infinitely large, they “blow up” and as they approach 0, they decay. They do so at different rates: for instance in function c, as x approaches infinity (positive and negative), it decays to 0, however when approaches 0, from the left or right it approaches positive and negative infinity respectively.
Asymptotic Comparison
As will be much larger than . Write asymptotically dominates . In other words… which is to say that constants don’t have much bearing on the magnitude of the overall number. Thus, As :
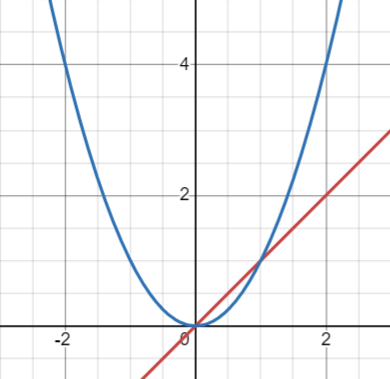
So as approaches infinity, it does not matter what the constant is.
Similarly, As and
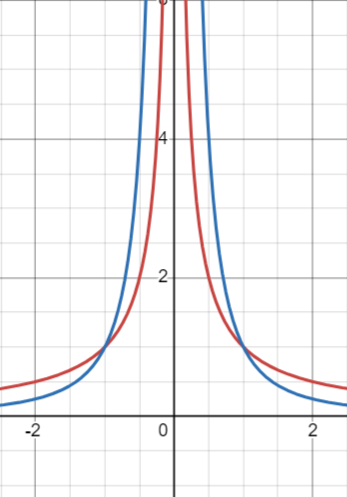
Where the red function is and the blue function is
Any exponential growth is much greater than a power law. To get a better idea of asymptotic dominance as : Generally, , blows up slower than any power law (And any power law grows slower than any exponential law) as
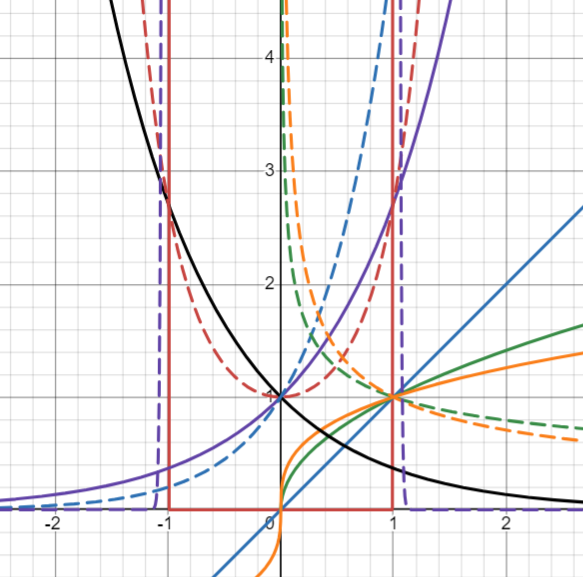
As for ,
(Solid red then blue then green then orange then (1) purple then black then dashed version) - Observe the behavior at 1