Relativistic momentum

For small velocities (relative to the speed of light), $p=mv$ is a valid approximation to make. If the following collision occurred in the frame of reference of an object that was moving at a high speed, then …

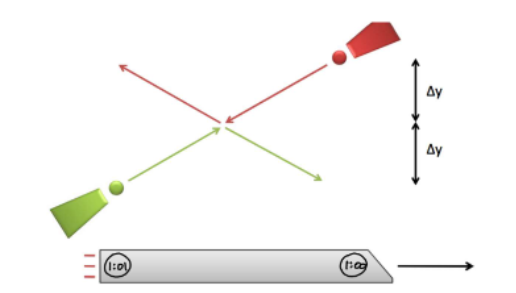
becomes …

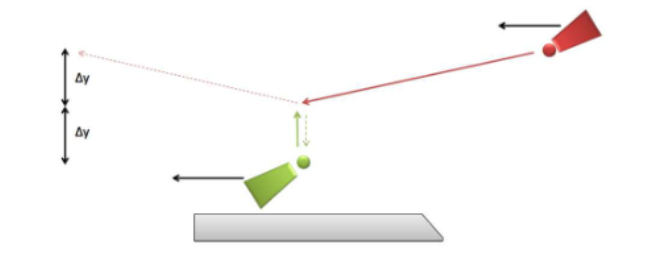
In the frame of the ground, the momenta of the balls would cancel, but from the frame of the train, the momenta would not. Take a small y velocity for the green ball, and a velocity comparable to the speed of light for the red ball. If clocks were attached to the balls, then the red ball would be running slowly by a time dilation factor of $\gamma$. With this the following can be ascertained:

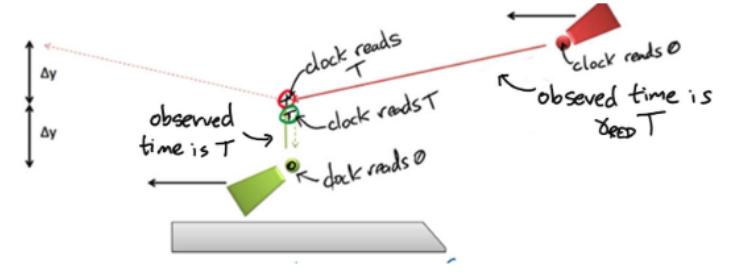
Where: $|p_y^{RED}|=|p_y^{GREEN}|=m{v}_y^{GREEN}={\gamma }^{RED}m{v}_y^{RED}$ Thus, $\vec{p}=\gamma m\vec{v}$ With the relativistic formula for momentum, momentum is still proportional to an object’s mass and is in the same direction as the objects velocity, but it is no longer just proportional to velocity. In fact, as the speed of an object approaches the speed of light, the momentum of the object goes to infinity! Once we have this correct formula for momentum, momentum conservation works the same way as
before. The sum of momenta for a collection of objects before a collision must be equal to the sum of the momenta of the objects after the collision, and this will be true in any frame of reference.