Simple Harmonic Motion (SHM)

Overview

Oscillations are periodic motions which center around an equilibrium position. Simple harmonic motion (SHM) is a special type of oscillation. For example:

The simple pendulum
The vibration of strings in a violin
The spring-mass system, where the mass is initially displaced to produce a periodic motion around the equilibrium position

An object undergoes SHM if it experiences a force which is proportional and opposite of the displacement from its equilibrium position. The period is independent of the amplitude of the SHM and can be given by the following equation.

For a pendulum:

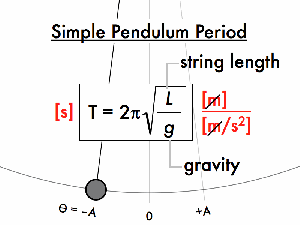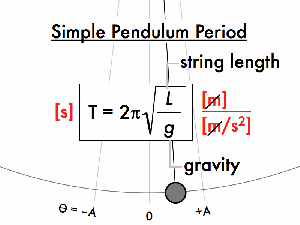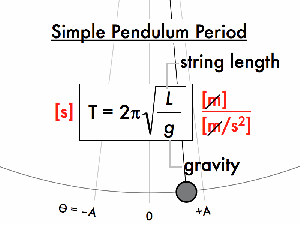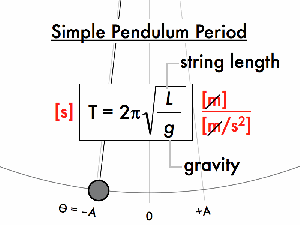
For a spring-mass system:

Time, Period, frequency, Amplitude, Displacement, and Phase Difference

Displacement (x)	Amplitude	Period (T)	Frequency (f)	Phase difference
Displacement of the oscillating object at a specific time from its equilibrium position	Maximum displacement of the oscillating object	Time taken for one complete oscillation (in seconds)	Number of times the object oscillates per unit time (usually one second). f=1/T	The difference between two SHMs with the same frequency in terms of their relative position in a cycle measured in radian

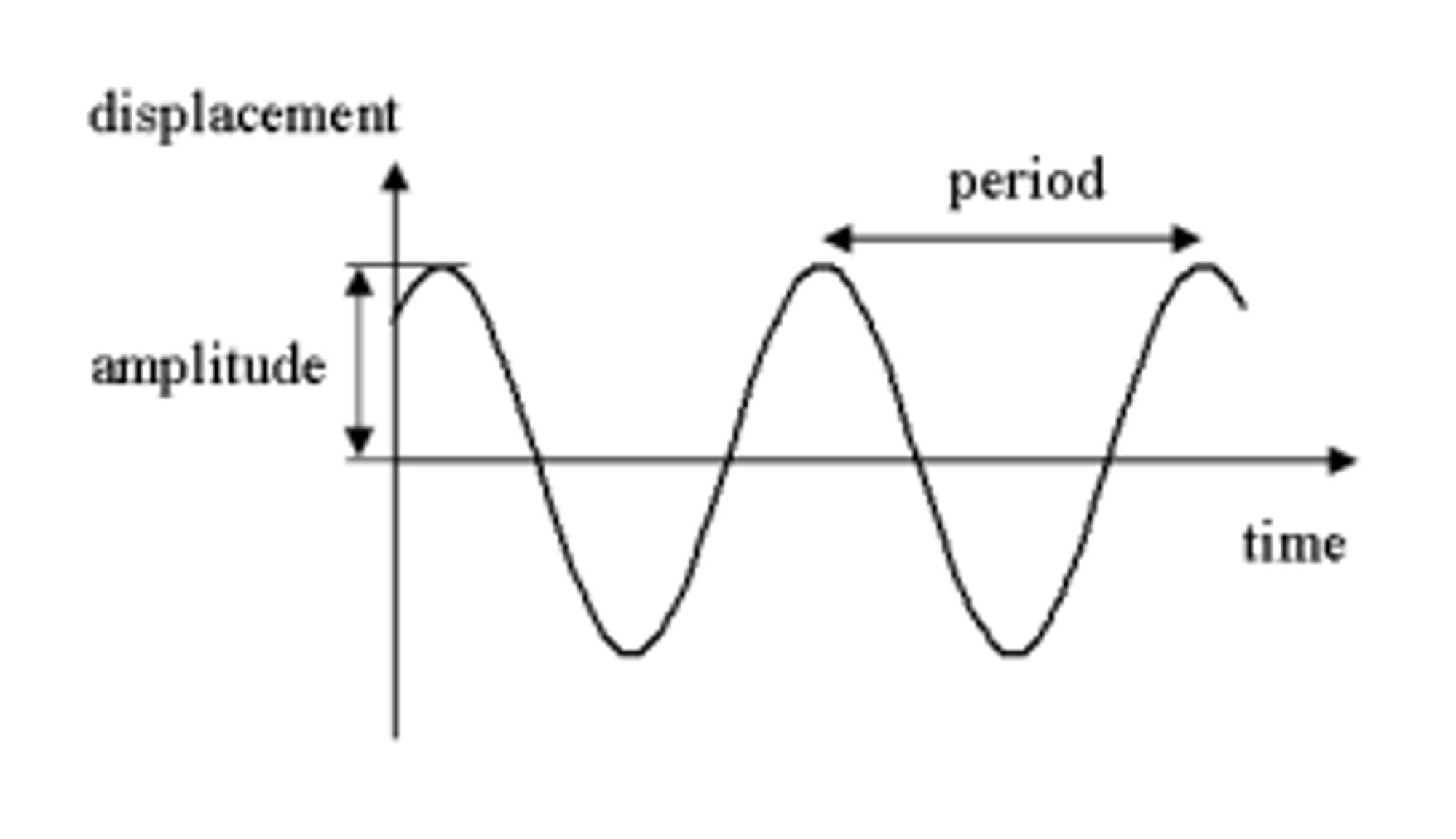
Conditions for Simple Harmonic Motion

When the body is displaced from equilibrium, there must exist a restoring force (a force that wants to pull the body back to equilibrium).
The magnitude of the restoring force must be proportional to the displacement of the body and acts towards the equilibrium.

Travelling Waves

A travelling wave is a continuous disturbance in a medium characterized by repeating oscillations. For example:

A rope that is flicked up and down continuously creates a repeating disturbance similar to the shape of a sine/cosine wave. Energy is transferred by waves. Matter is not transferred by waves. The direction of a wave is defined by the direction of the energy transfer.

Wave, Frequency, Period and Wave Speed

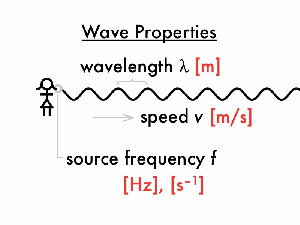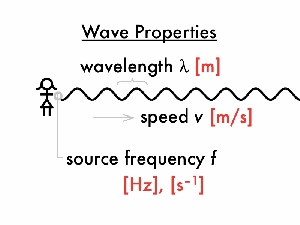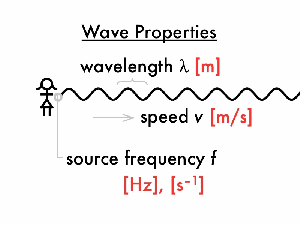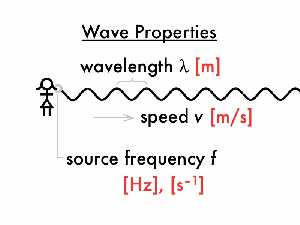Wavelength, frequency, and period follow the same rules of SHM. Wave speed can be calculated by the following equation $v = f λ$ Where $v$ is velocity in $m / s$ , $f$ is frequency in $Hz$ and $λ$ is wavelength $m$ .

Transverse and Longitudinal Waves

Longitudinal waves are made of compressions and refractions where the oscillations of the wave are with the direction of the wave; where transverse waves are waves that have their oscillations move perpendicular to the wave’s direction.

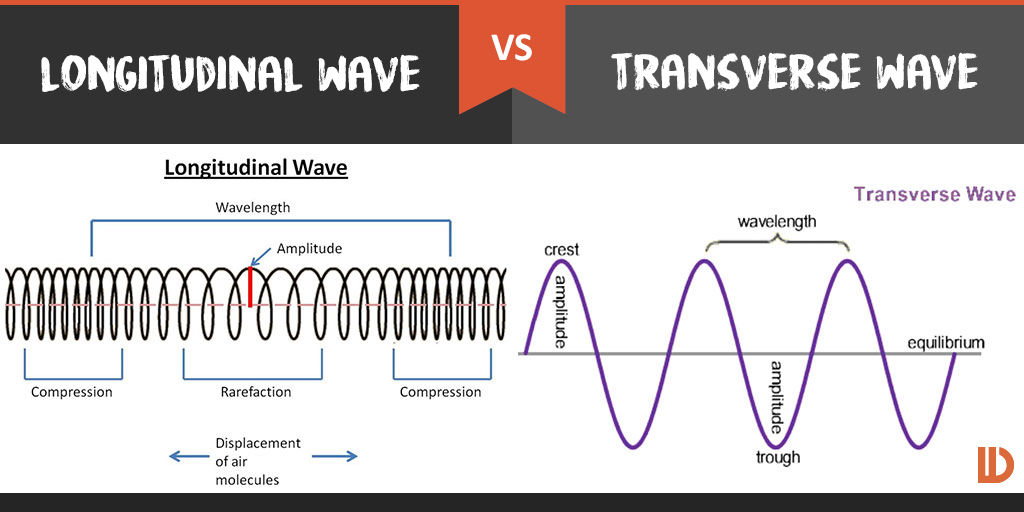
The direction of oscillation is perpendicular to the direction of the wave. Example: Water waves, Wave in a string flicked up and down, Light (electromagnetic waves). = A point with maximum positive displacement is called a crest. A point with minimum displacement is called a trough.

The direction of oscillation is parallel to the direction of the wave. Example: Wave produced in a spring, Sound waves, Earthquake P-waves = A region where particles are closed to each other is called a compression. A region where particles are furthest apart from each other is called a rarefaction.

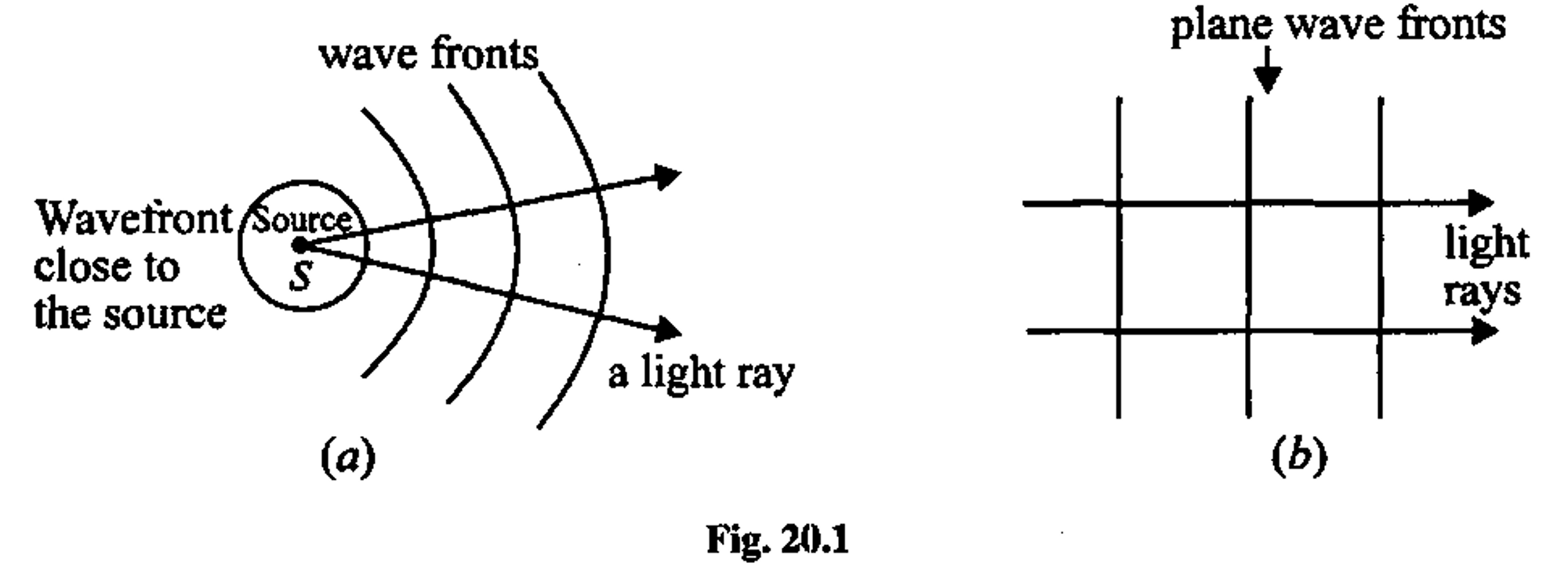
Wavefronts and Rays

Wavefronts:

Lines joining points which vibrate in phase.
Can be straight lines or curves.
The distance between successive wavefronts is the wavelength of the wave.

Rays:

Lines which indicate the direction of wave propagation.
Rays are perpendicular to wavefronts.

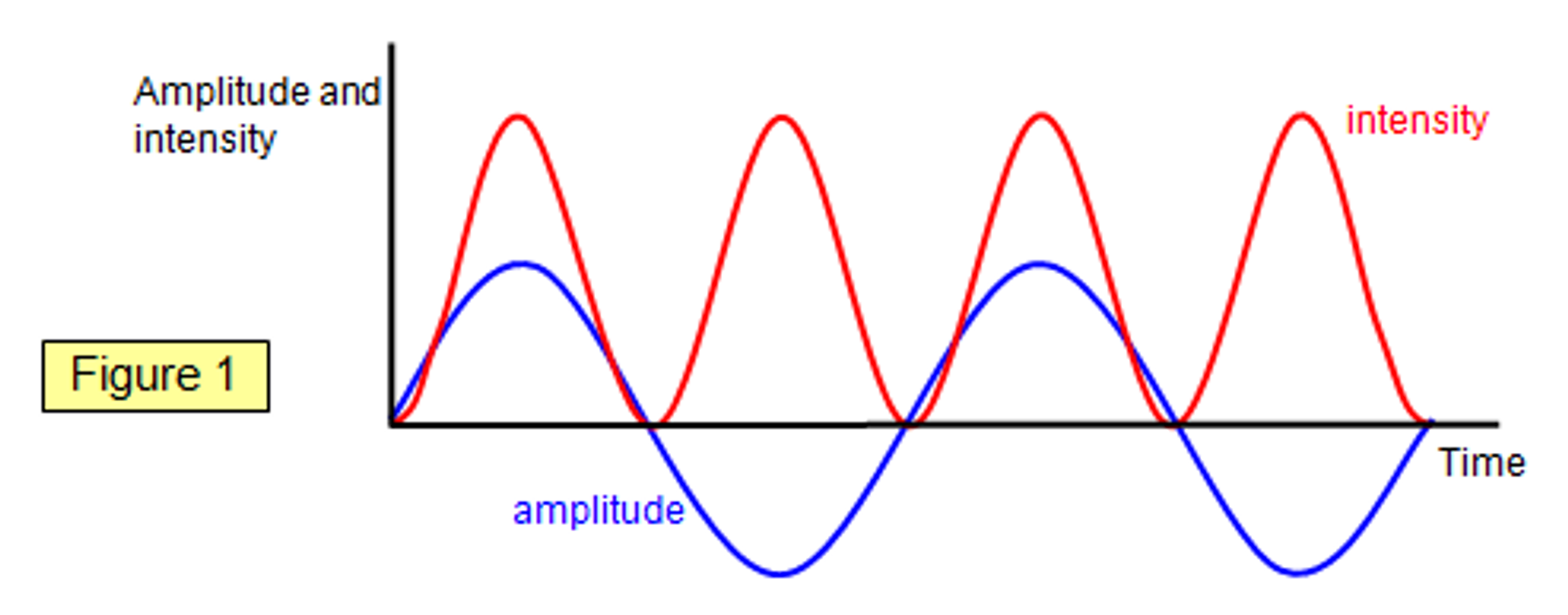
Amplitude and Intensity

The amplitude and intensity of a wave depends on its energy. The intensity of a wave is proportional to the square of its amplitude (I∝A^2).

Superposition, Fourier’s Theorem

The principle of superposition states that the net displacement of the underlying medium for a wave is equal to the sum of the individual wave displacements.

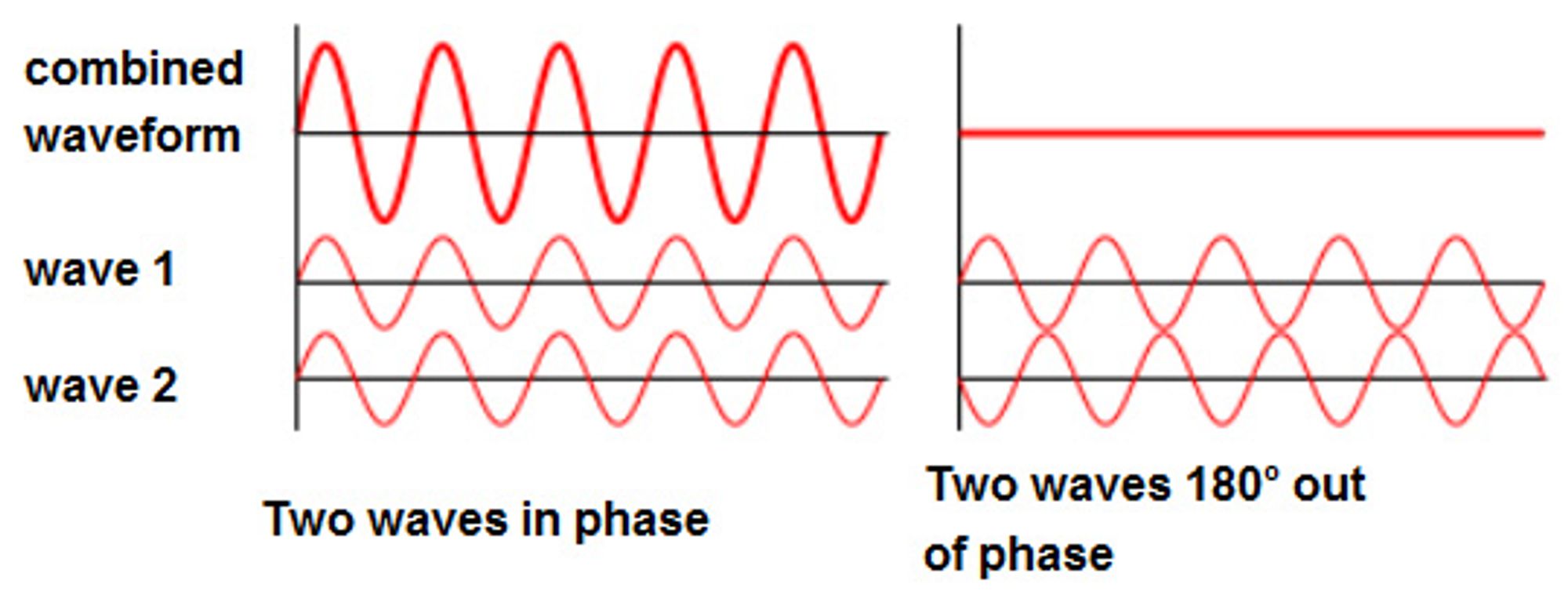
The left shows constructive interference (superposition) where the two waves add up (e.g. 1+1=2). The right shows deconstructive interference (superposition) where the two waves cancel each other (e.g. 1+(-1)=0).

Doppler Effect

For longitudinal waves, if the source of the waves is moving while emitting a wave, the apparent wavelength will change depending on the speed of the moving object, wavelength, distance etc.

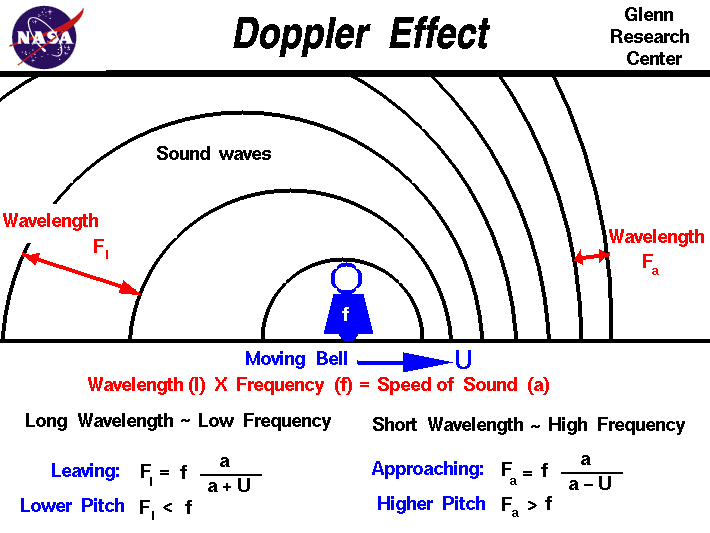
Depending on the scenario, there are 4 different formulas that come from the same formula: $f^{'} = \frac{v + v _{o}}{v + v _{s}} f_{s}$ Where $f^{'}$ is the observed frequency of the wave emitted by the source received by the observer, $f_{s}$ is the original frequency of the wave, $v$ is the velocity of the wave, $v_{o}$ is the velocity of the observer, and $v_{s}$ is the source (object’s) velocity.

	Velocity of the wave	Wavelength of the wave	Frequency of the wave
Moving observer	Changes	Constant	Changes
Moving source	Constant	Changes	Changes
Frequency observed changes according to the equation $v = f λ$ .
The Doppler effect for electromagnetic waves is as follows:
$Δ f = \frac{v}{c} f$ Where $Δ f$ is the change in frequency of the wave received by the observer as compared to the original frequency emitted by the source, v is the velocity of the observer, c is the speed of light, and f is the original frequency of the wave.

This equation should only be used when the velocity of the observer is much smaller than the speed of light
Add Δf to f to obtain the observed frequency (f’) when the wave source and the observer are moving towards each other.
Subtract Δf from f to obtain the observed frequency (f’) when the wave source and the observer are moving away from each other.

Application of the Doppler effect in speed detectors:

A beam of electromagnetic wave is fired at the car.
The frequency of the reflected wave is compared to that of the original wave beam. A higher frequency indicates that the car is moving towards the detector and a lower frequency indicates that the car is moving away from the detector.
The speed of the car is calculated from the extent of shift in frequency by v=fλ.

Take note that the overall difference in frequency is 2Δf from the equation because the wave travels to the car and then back to the speed detector.

Electromagnetic Waves

To see more see Electrodynamics.

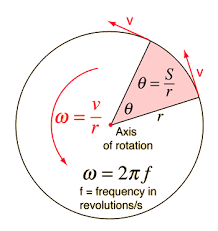
The angular velocity, $ω$ is related to the period of the SHM by the following equation $ω = 2 π f = \frac{2 π}{T}$ Where $ω$ is the angular velocity of an oscillating object ( $m / s$ ), $f$ is the frequency of an oscillation ( $h z$ ) , and $T$ is the period of the oscillation ( $s$ ).

By Newton’s Second Law, SHM can be defined as the following equations:

General SHM equation applies to all simple oscillating systems: $a = - ω^{2} x$
For a system starting at equilibrium: $x = x_{0} sin (ω t)$ ; $v = ω x_{0} cos (ω t)$ ; $a = - ω^{2} x_{0} sin (ω t)$
For a system starting at maximum displacement: $x = x_{0} cos (ω t)$ ; $v = - ω x_{0} sin (ω t)$ ; a = -\omega ^2 x_0 \cos (\omega t) Where $x_{0}$ is the amplitude (maximum displacement), $x$ is the displacement, $v$ is the velocity, and $a$ is the acceleration.

🪴 Quartz 4.0

Explorer