Base n number systems

2024-07-3013:28 Status:NESCS50 Tags: Number Theory

We typically use base 10 systems to represent numbers in common application. In certain cases, it is more economic to use a different number system to be more efficient (condensing information). The inverse can be true as well:

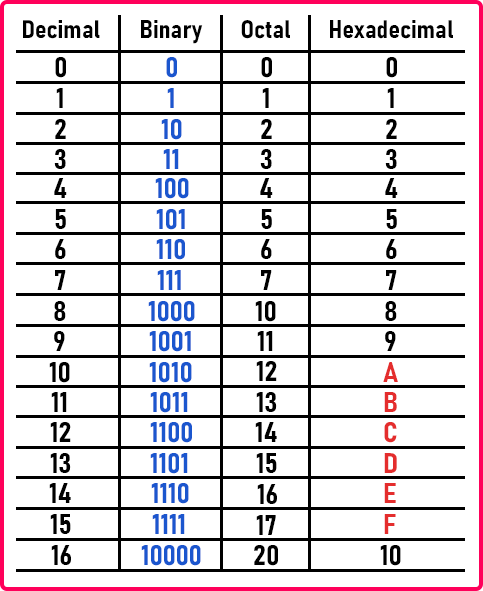
Binary (Base 2)

In cases where 10 separate states can be difficult to differentiate, binary is often used. (100% on to 90% on to 80% on to … 10% on to 0% on is more difficult to implement than 0% on or 100% on = transistors in computers). Binary (or sometimes referred to as assembly/machine code):

• 0s and 1s = on and off, Binary = a pattern of on/off switches (aka transistor)
• e.g. 0101 (in binary)= 5(in decimal)
• ASCII = assigning binary values to symbols and characters → the newer code = Unicode to include characters (16 bits) 65 thousand characters → Unicode universalizes the meaning of codes to characters (and its up to the manufacturer of a device to visualize, whether it be emojis (android vs. apple) or font) As computers are built on the simple on/off paradigm, they can be assigned to 1 and 0. With further extrapolation, these 0s and 1s can be used to represent other data.

Hexadecimal (Base 16)

In cases where base 10 is not condensed enough, base 16 is typically used as $2^4$ is useful in converting to other bases and already exponentially increases the amount of information in a single character. For instance, it is commonly used in describing color: RGB  = __ __ __ (decimal system) F= full, 0 = nothing → HEX = 1,2,3,4,5,6,7,8,9,A,B,C,D,E,F (e.g. 00FF00 = green, FFFFFF =  white)

Source(s)