Basics of quantum mechanics

2024-10-1313:25 Status:CHEM121 Tags: Quantum mechanics

Quantum mechanics is a theory that allows us to compute the properties of waves that describe particles. From the de Broglie equation, we expect that quantum particles will exhibit wave-like behavior.

Wavefunctions ($\Psi$) are mathematical representations of this wave-like behavior. The wavefunction contains all the information that can be obtained from a quantum system in a given state. This is a direct result of Heisenberg’s Uncertainty Principle in which either the position, or momentum of a particle be really known:

The probability of finding a particle is not directly given by the wave function but its square, $\Psi$ as it may be negative. Thus, we square it, ${\Psi }^2$.

Schrödinger Equation

The Schrödinger equation is the quantum mechanical analogue to Newton’s law for classical mechanics. It has the general form of: $\hat{H}\Psi =E\Psi$Where $\hat{H}$ is the Hamiltonian, which includes kinetic and potential energy terms, $\Psi$ is the Wave function, and $E$ is the Energy. The Hamiltonian will depend on the physical situation of the quantum system; they are not as straightforward as their classical analogues.

The Schrödinger equation for a quantum particle in one-dimension is: $-\frac{h^2}{8{\pi }^{2}m}\cdot \frac{d^2\Psi (x)}{d{x}^2}+V(x)\Psi (x)=E\Psi (x)$ Where $h$ is Planck’s constant, $6.626\times 10^{-34}Js$, $m$ is the mass of the particle, $x$ is the position of the particle, and $V$ is the potential energy. (This is the simplified equation, as it only includes one dimension and does not account for time). And $E$ is the total energy observed.

For example, in a hydrogen atom, the electron is moving in the Coulomb field of the proton. In the case, $V$ is the potential energy of the electron from the Coulombic force between the nucleus and electron. If we consider a particle that is moving in free space without any external forces, then the potential energy is zero. What is important to keep in mind is that potential, $V$ will depend on the problem we consider.

Principle Quantum Number

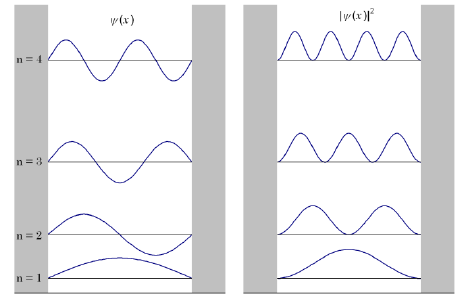
In order for $-\frac{h^2}{8{\pi }^{2}m}\cdot \frac{d^2\Psi (x)}{d{x}^2}+V(x)\Psi (x)=E\Psi (x)$ to be true, $\Psi$ must be a mathematical function whose second derivative gives the same function, $\Psi$ back, multiplied by a constant. There are 3 equations that satisfy this definition, two of which are sinusoidal. While $\sin (kx)$ and $\cos (kx)$ both satisfy the Schrödinger equation, only $sin(kx)$ is 0 at x= 0. $\Psi =A\sin (kx)$Where $A$ and $k$ are constants, we also know that there is an infinite wall at $x=L$, which means that the wavefunction of the particle must be 0 at $x=L$, thus: $\Psi (x=L)=A\sin (kL)=0$ The values of $k$ satisfy $\Psi (L)=Asin(kL)=0$ are: $kL=n\pi$ Where $n=1,2,3,...$ is the principle quantum number. (Note that if $n=0$, then $k=0$ and thus $\Psi =0$ everywhere, then the total probability of finding the particle is 0, and is ultimately not a physically acceptable solution to the Schrödinger equation). To make the wave function have fixed ends at the same height, $k=\frac{n\pi }{L}$ $n$ describes different states of the quantum system and is a natural number. In order for the probability to be 1 in a 1-D box, the amplitude of the wave function must be: $A=\sqrt{\frac{2}{L}}$As the distribution is normalized to ${\Psi }^2$. When substituting all constraints: ${\Psi }_n(x)=\sqrt{\frac{2}{L}}\sin (\frac{n\pi x}{L})$

Energy Quantization

The energy of a particle, $E_n$ can be found by solving the Schrödinger equation with the wave function of ${\Psi }_n(x)=\sqrt{\frac{2}{L}}\sin (\frac{n\pi x}{L})$. Since $n$ can only be natural numbers not including 0, the energy can only be specific values (quantized).

Each number “encodes” the state of the particle. Where $n=1$ is the ground state. The difference between the energy in the ground state and 0 is the zero-point energy. If $n$ is greater than 1, then it is considered to be excited.

Transitions Between Energy Levels

Quantum particles exist in certain states, so excitation in their energy levels can be described as the difference in the difference of their energies: $\Delta E=E_{final}-E_{initial}=\frac{h^2{n}_f^2}{8m{L}^2}-\frac{h^2{n}_i^2}{8m{L}^2}=\frac{h^2}{8m{L}^2}(n_f^2-n_i^2)$ Where $\Delta E$ is the change in energy for the system, $E_{initial}$ is the initial energy of the system, and $E_{final}$ is the final energy of the system. If $\Delta E$ is negative, then the system emits energy, if positive, then the system absorbs energy. This is the reason why all particles have unique absorption/emission spectra. For more see Atomic structure.

Superpositions of Wavefunctions

Similar to waves, wave functions undergo constructive and destructive interference. Wavefunctions can be combined by taking the sum of the wave functions at different states where each has a different coefficient: $\Psi =c_1{\Psi }_1+c_2{\Psi }_2+c_3{\Psi }_3...$The wavefunction resulting from interference is called a superimposed wave function. The most notable property is that it will have a different probability distribution to its component wave functions.

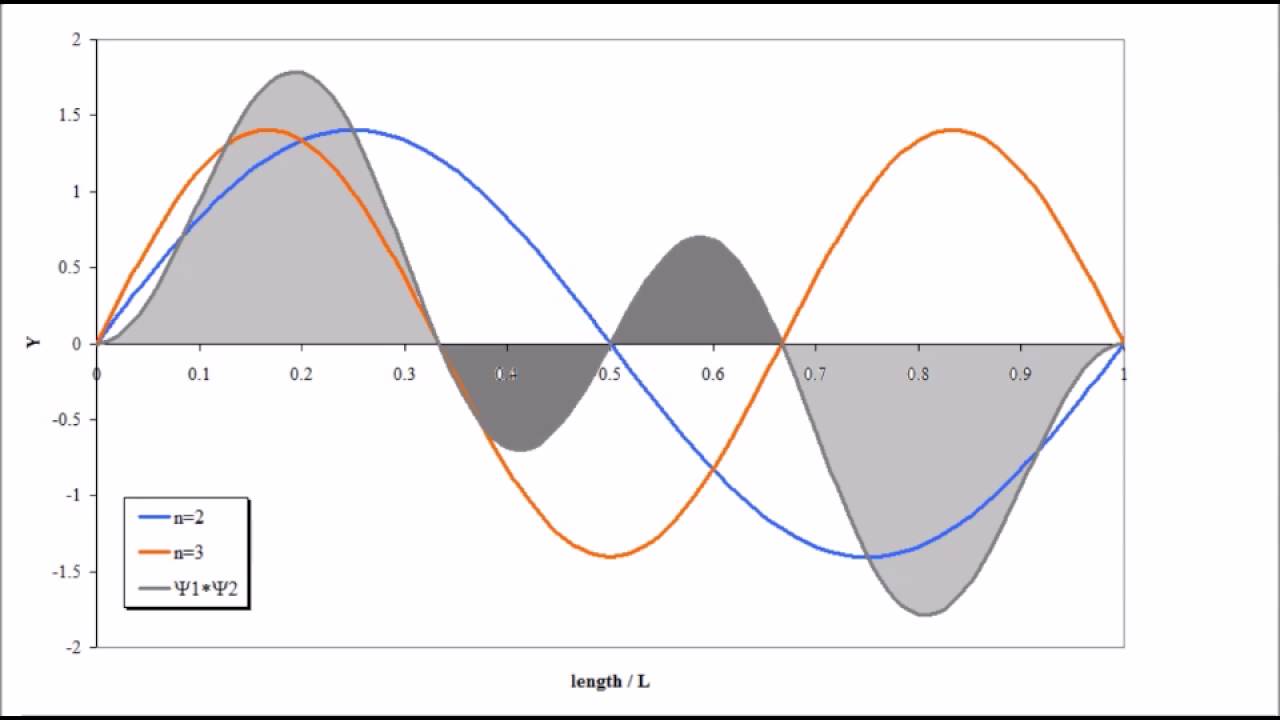
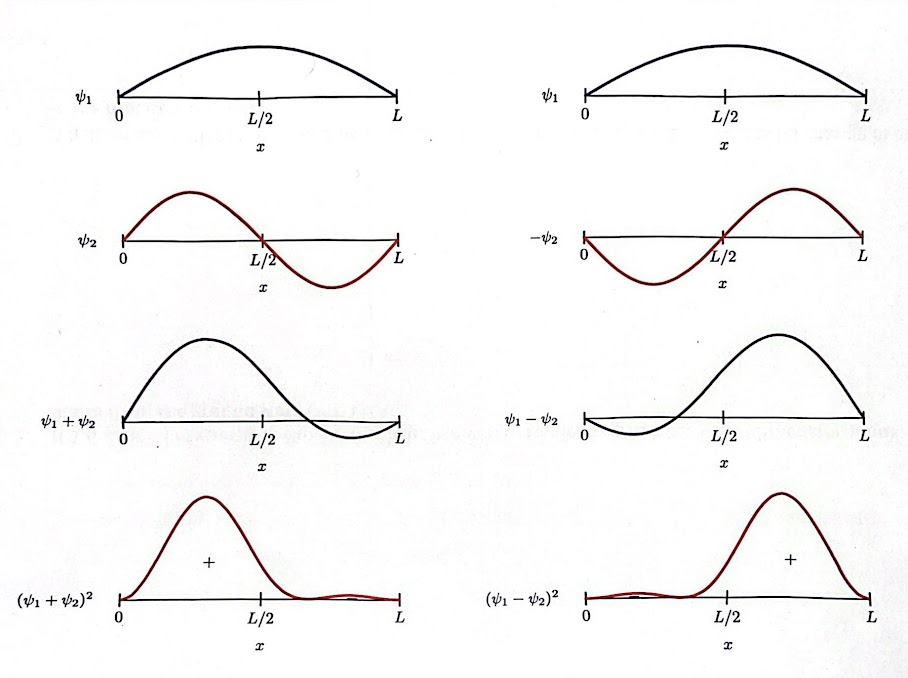
• These graphs imply a convergence.
• Whenever a quantum particle is confined, it is quantized.

Review

• Quantization arises from confinement. Thus, the energy of a particle in a one-dimensional box is quantized.
• The energy of a particle in a one-dimensional box is dependent on the principle quantum number, $n$ the mass, $m$ and the length of the box, $L$.
• The wavefunction and energy states are labelled by quantum numbers, which for the particle in a box are the positive integers.
• The lowest energy possible for a particle is a one-dimensional box is the particle at its ground state, $n=1$.
• The wavefunction, $\Psi$ has $n-1$ nodes.

The particle in a box model provides us with a wave function of a particle, a formula for energy and the definition of the ideas of energy quantization, nodes and probability distributions, We used the particle in a box model to determine characteristics of the system and to discuss how systems interact.