Kinematics

2024-06-1500:53 Status:Complete

Kinematics is a branch of Classical mechanics that describes the motion of points, objects and systems of groups of objects without reference to the causes of motion. For further applications of kinematics see Mechanics as it deals with tangible manipulation of kinematics to redirect energy. Simple Harmonic Motion (SHM)

Fundamentals

Distance and Displacement

• Distance (Scalar): A scalar quantity which measures how far two locations are apart from each other along a certain path.
• Displacement (Vector): A vector quantity defined by the length and direction of the line segment joining the initial and final positions of an object. (m) with direction

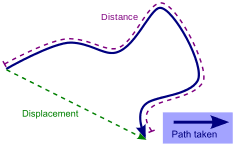
When considering directions, these may be composed of x, y, and z components, so often to manipulate Vectors they must be first expressed in x, y, and z before they can be reconstructed into a resultant vector.

Speed and Velocity

• Speed (Scalar): Rate of change of distance to time. (m/s); no direction (instantaneous is at any point in time)
• Velocity (Vector): Rate of change of displacement to time. (m/s): with direction (instantaneous is at any point in time) Velocity is a measure dependent on the motion of the observer. The relative velocity of A to B is equal to the vector subtraction of the velocity of B from the velocity of A.

There are a few different forms of each to describe slightly different scenarios.

• Average speed = ratio of total distance to time: $averagespeed=\frac{totaldistance}{time}$

• Average velocity = ratio of displacement to time: $averagespeed=\frac{displacement}{time}=\frac{\Delta x}{\Delta t}=\frac{x_2-x_1}{t_2-t_1}$

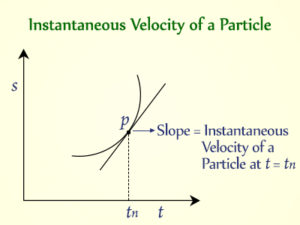
• Instantaneous variations happen at a specific point: - for more see Derivatives

• Tangential variations also occur at a specific point relative to neighboring points (without the need for calculus):

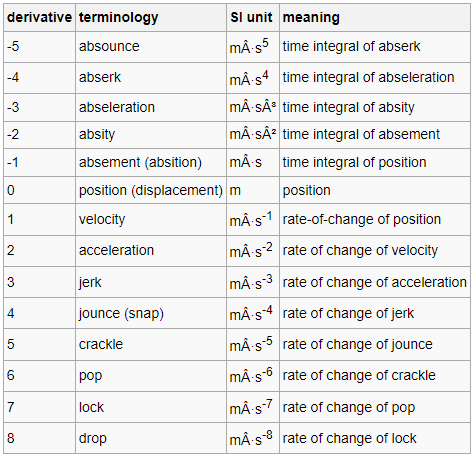
Acceleration and Higher Order Derivatives

• Acceleration is a measure of a change of velocity. ($m/s^2$) = $\bar{a}=\frac{v-v_0}{t}=\frac{\Delta v}{\Delta t}$
  Acceleration due to gravity of any free-falling object is given by g=9.81m/s^2. This value does not depend on the mass of the object.

Take note that acceleration is a vector and thus has a direction. If we assume the upwards direction to be positive, the acceleration due to gravity would have a negative value of g=-9.81m/s^2.

Jerk is the measure of the change of acceleration and is measured in $m/s^3$ = $\frac{d^{3}s}{d{t}^3}$, Snap (jounce) is the measure of the change of jerk and is measured in $m/s^4$ $\frac{d^{4}s}{d{t}^4}$, Crackle is the measure of the change of snap and is measured in $m/s^5$ $\frac{d^{5}s}{d{t}^5}$, Pop is the measure of the change of crackle and is measured in $m/s^6$ $\frac{d^{6}s}{d{t}^6}$etc.

Because each order is being derived with respect to time, it follows that each can be “undone” by integrating: Displacement can be found by integrating a finite velocity function, velocity can be found by integrating a finite acceleration function etc. Moreover, graphs can represent these functions and their integrals:

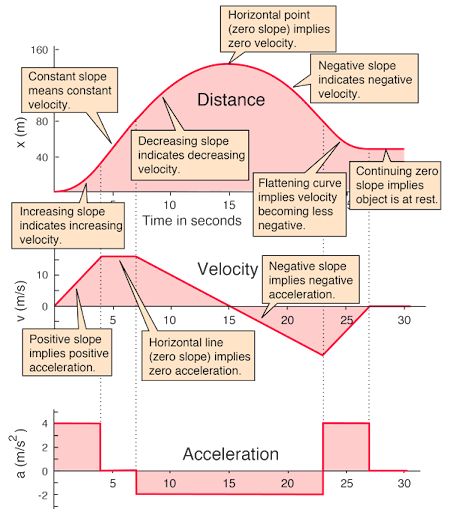
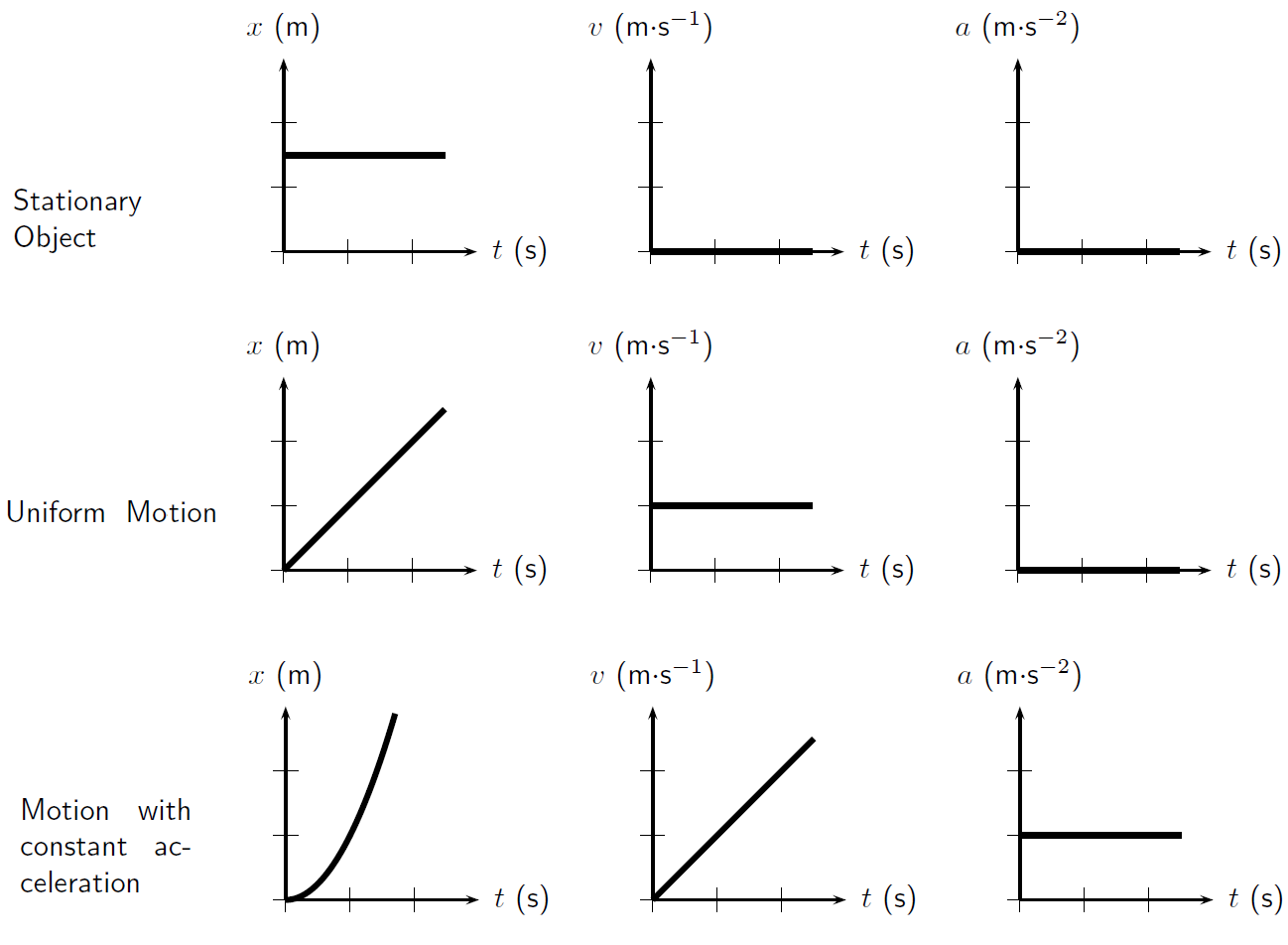
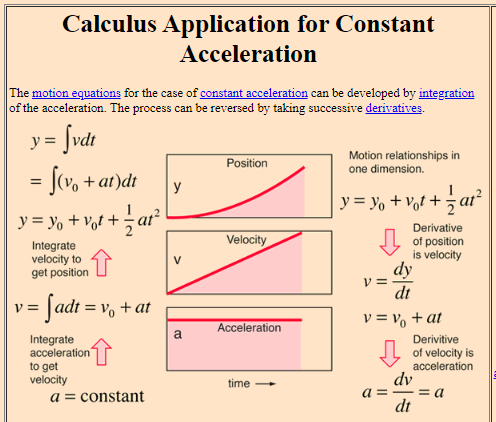
Formulas for Uniform Acceleration

Derivation of formulas with constant acceleration: https://openstax.org/books/university-physics-volume-1/pages/3-4-motion-with-constant-acceleration. $v=at$ $s=ut+\frac{1}{2}a{t}^2$ $s=\frac{1}{2}(u+v)t$

$v^2=u^2+2as$ Where $s$ is the displacement of an object, $u$ is the initial velocity, $v$ is the final velocity, $a$ is acceleration and $t$ is time.

Projectile Motion

If air resistance is negligible in a projectile motion, only the acceleration of gravity is considered. The horizontal component of velocity is constant; the vertical velocity accelerates downwards at $9.81m/s^2$; when the projectile reaches its maximum height, its vertical velocity is zero; and the trajectory is symmetric.

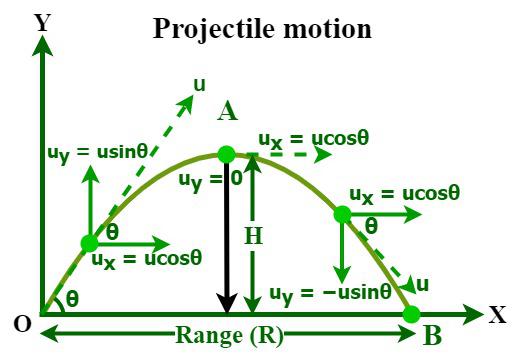
If air resistance is considered, the trajectory of the projectile changes to the following: The maximum height of the projectile is lower; the range of the projectile is shorter, and the trajectory is no longer symmetric; horizontal acceleration must also be considered.

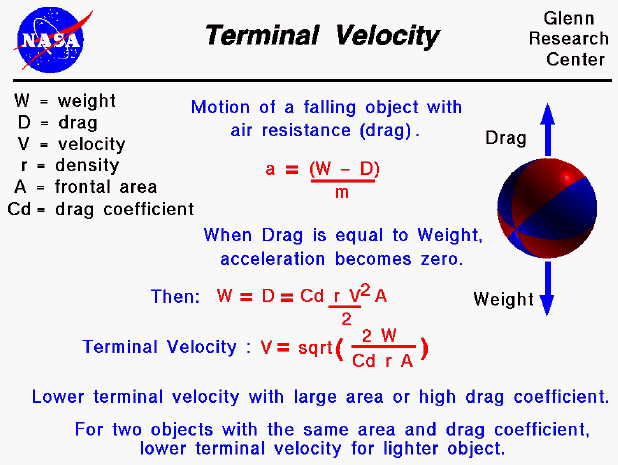
Fluid Resistance and Terminal Speed

Air resistance limits the maximum velocity an object could attain from free-falling. For example:

• If you jump out of a plane and undergo free-falling, you will feel an upward force exerted on you by the surrounding air due to air resistance.
• As you fall faster and faster due to gravity, this upward force exerted by air becomes greater and greater until it balances your weight. At this point, the net force acting on you becomes zero, and you no longer accelerate.
• This specific velocity at which you stop accelerating during a free-fall is called the terminal velocity.

Forces

If objects are considered to be point particles, then the center of mass of an object is considered over the actual distribution of weight. The unit of force is a newton, $N$. Objects are represented as a point mass to enable the representation of forces as arrows in free-body diagrams.

Free-Body Diagrams

On a free body diagram, forces acting on an object are represented as arrows which stem from a point mass. The length and direction of the arrows corresponds to the magnitude and the direction of the forces acting on the body of interest. E.g.

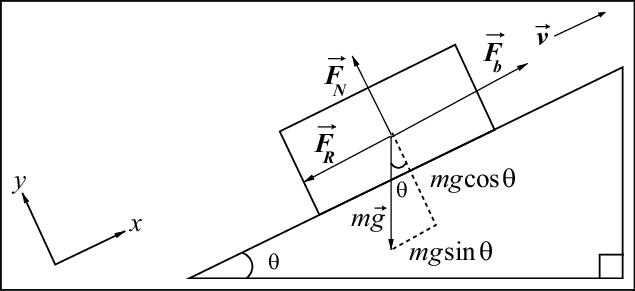
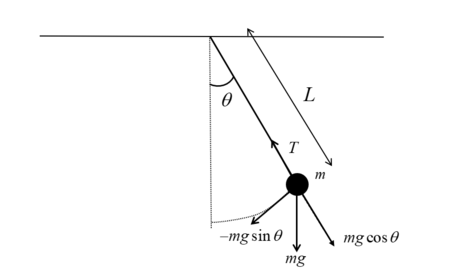
These diagrams can be useful in determining the motion and acceleration of an object:

1. Resolve all acting forces into horizontal and vertical components: Make diagonal forces into their x, y, z components.
2. Add up all components in the same dimension: e.g. if pushing down on a table, add the force of the push and the force of gravity.
3. Recombine the x, y, z components to create a resultant force.

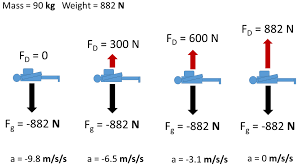
Elevator Free-Body Diagrams

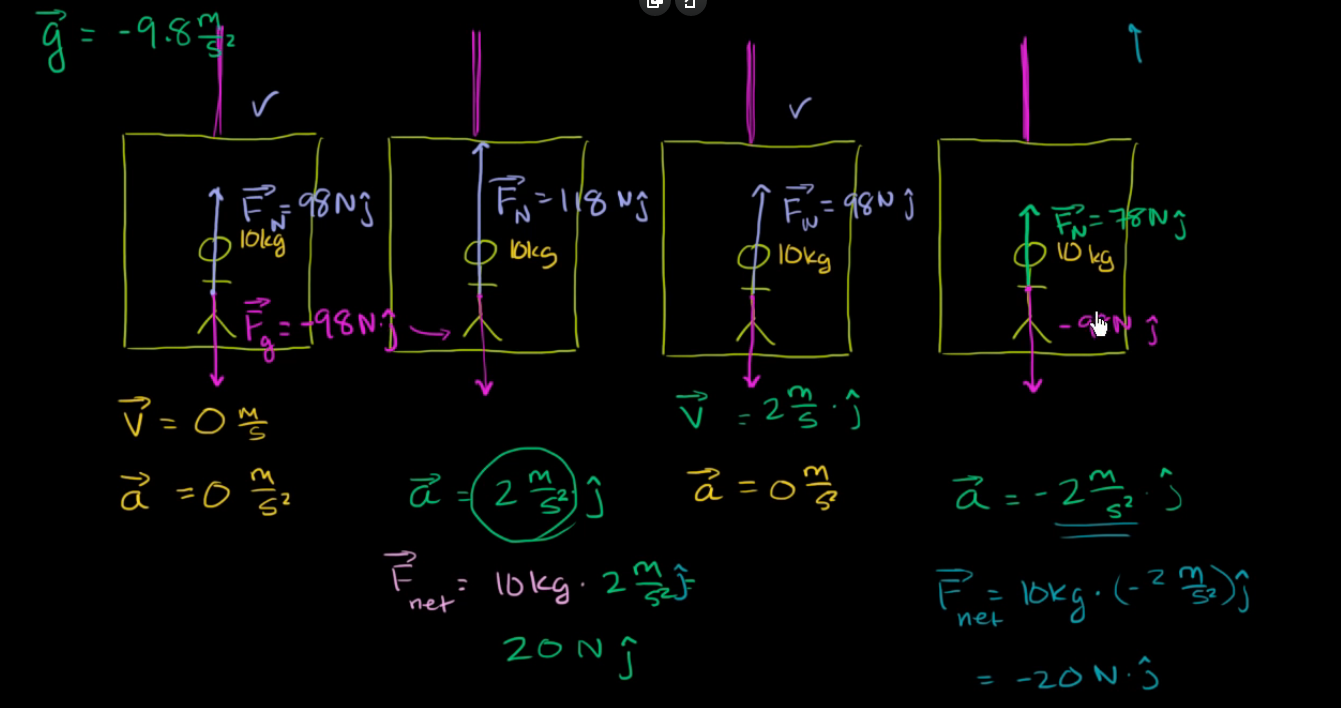
Transitional Equilibrium

A body is said to be in translational equilibrium if the net force acting on the body is zero. This means the body is either at rest or travels at constant velocity. For example:

• Mass hanging at rest
• Elevator moving upwards at constant velocity
• Parachutist reaching terminal velocity

Newton’s Laws of Motion

1. Newton’s First Law (Law of Inertia) states that a body remains at rest or travels with constant speed along a straight line unless acted upon by an external force. (Net force = 0)
2. Newton’s Second Law states that net force is directly proportional to acceleration and to mass. (F=ma) $F=ma$
3. Newton’s Third Law states that if a body A exerts a force on body B, then body B exerts a force of the same magnitude but in the opposite direction of body A.

This pair of forces is called an action-reaction pair, which must act on two different bodies.

Solid Friction

Friction is a non-conservative force which opposes motion. If there is no motion, then there will be no force caused by friction.

For two solid surfaces moving over each other, the friction will be affected by the nature (roughness etc.) of the two surfaces. However, the surface area and velocity of the object does not affect the friction.

There are also two types of friction for solid surfaces: static friction and kinetic friction. Static friction is that which stops objects from beginning to move. Kinetic friction is that which slows objects down when they are moving. Static friction is always larger than kinetic friction.

These two types of friction are defined individually by their constants µs and µk respectively.

The forces of friction are also dependent on the normal force the surface is applying, leading to Friction force (static) =< µs * Normal force for objects that are not moving and Friction force (static) = µs * Normal force for objects that are moving.

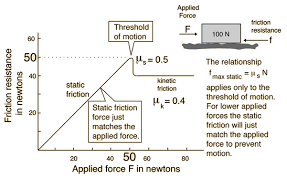
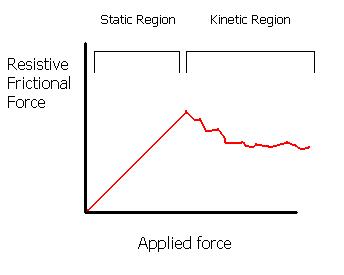
Normal Force

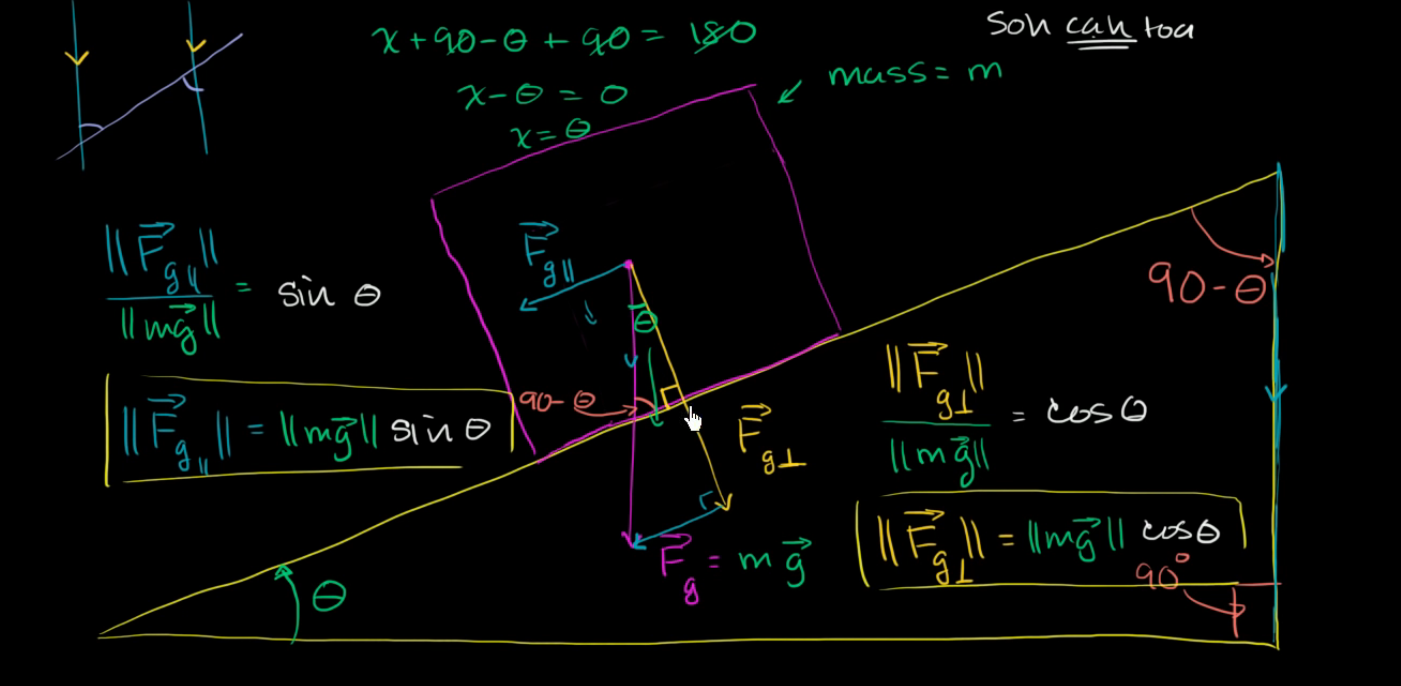
The normal force is the component contact force perpendicular to its surface. This force is closely linked to Newton’s third law that states, that an object must experience an equal but opposite reaction. When considering the weight of an object, there must be a normal for to keep it stationary (assuming a = 0)

Inclined Plane

Hooke’s Law

Hooke’s law is an empirical law that states that the force, $F$ required to extend or compress a spring scales linearly with respect to the distance of extension or compression: This can be expressed with the equation:

$F_s=kx$ Where $F_s$ is the force of spring, $x$ is the extension (small compared to the total possible deformation of the spring), and $k$ is a constant factor characteristic to the spring (its stiffness).

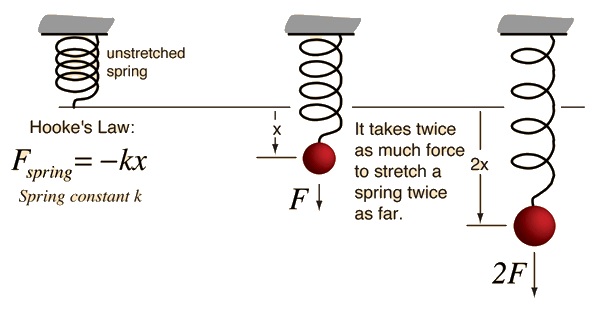
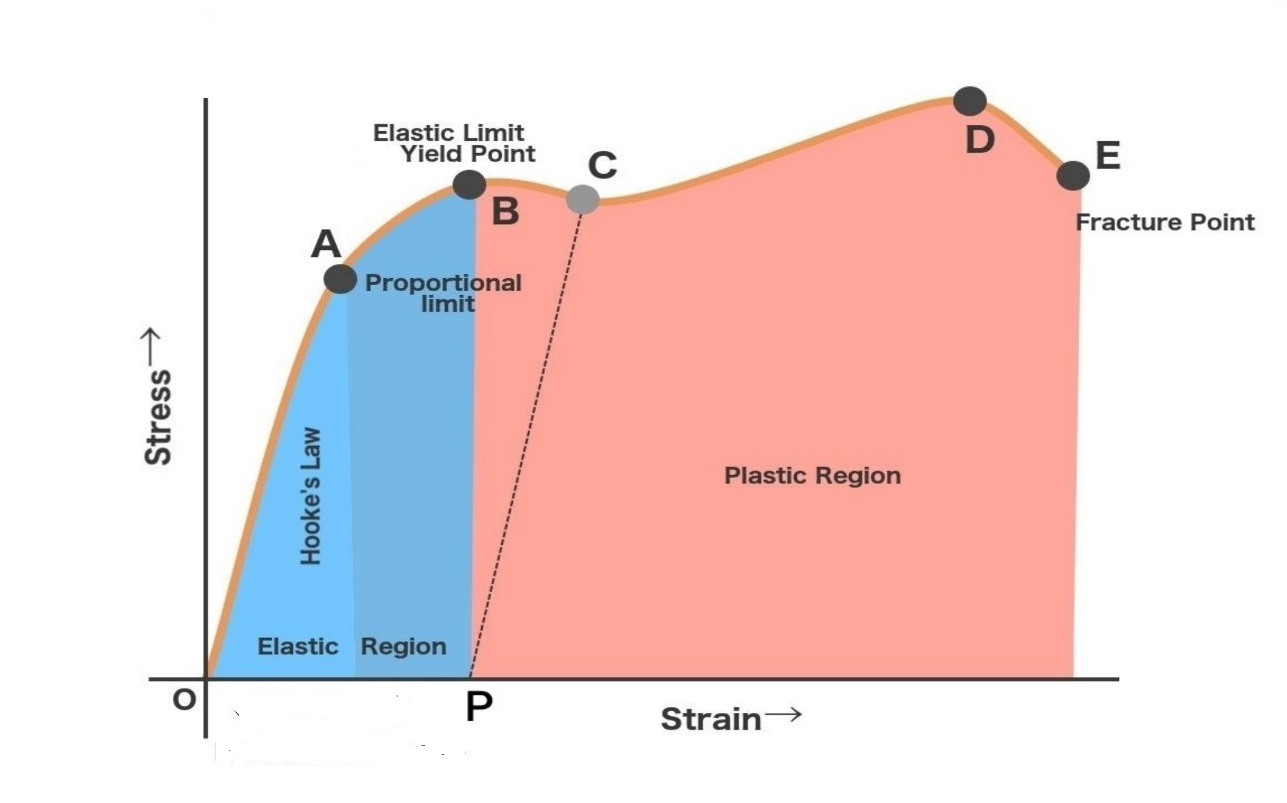
Hooke’s law only applies to a certain extent as there is a proportional limit and elastic limit The proportional limit is where the force exerted onto a spring is no longer proportional to its extension (or compression). The elastic limit is where the spring will not return to its original state. After a certain amount of strain, the spring will fracture/fail.

Energy

Conservation of Energy

There is a finite amount of energy in the universe and within a given system, energy is only converted from one form to another (never created or destroyed): $K_1+U_1=K_2+U_2$ Where $K_1$ is the kinetic energy of an object initially, and $K_2$ is at another point in time, and $U_1$ is the initial potential, and $U_2$ is the final potential energy.

Kinetic Energy

Kinetic energy ($E_K$, KE) is the energy of a body due to its motion and is given by the equation: $E_k=\frac{1}{2}m{v}^2$Where $E_k$ is the kinetic energy ($J,\frac{kg{m}^2}{m^2}$), $m$ is the mass of the object, $v$ is the velocity of the object.

Gravitational Potential Energy

The gravitational potential energy ($E_p,E_g,E_{gp}$, GPE) of an object changes with its height and is given by the equation: $E_p=mgh$Where $E_p$ ($J,\frac{kg{m}^2}{m^2}$) is the gravitational potential, $m(kg)$ is the mass, $g(m/s^2)$ is the gravitational field strength constant, $9.81m/s^2$, $h(m)$ is the vertical height of the object.

Elastic Potential Energy

Elastic energy is potential energy stored as a result of the deformation of an elastic object such as the stretching of a spring and is given by the equation: $E_p=\frac{1}{2}k{x}^2$ Where $E_p,E_k$ ($J,\frac{kg{m}^2}{m^2}$)is the potential energy, $k,(kg/s^2)$ is the spring constant, and $x,(m)$ is the extension of the spring.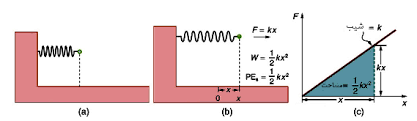

Work

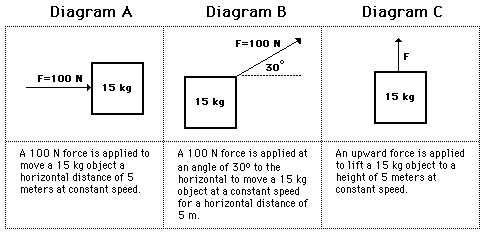
Work done measures the transfer of energy due to a force and is a scalar quantity. The work done $W$ by a force $F$ on an object is given by the equation: $W=F\cdot s\cdot cos\theta$ Where $F$ is the net force, $s$ is the displacement (including vertical, or non-relevant components), and $\theta$ is the angle between the force and the direction of motion.

Power

Power, $P$ is the work done or the energy output per unit time and is given by the equation: $P=\frac{W}{t}$ Where $P$ is power, $W$ is the work done, and $t$ is the time taken. For constant force acting on an object with constant velocity, the power is given by the equation: $P=Fv$.

Conservation of Energy

Energy can neither be created nor destroyed; it can only be changed from one form to another. For example:

• An electrical heater transforms electrical energy to thermal energy.
• A falling object transforms potential energy to kinetic energy.

Total energy of an isolated body remains constant. In other words, $\Delta E_k+\Delta E_p=0$

Efficiency

Efficiency is the ratio of useful energy output to energy input as a percentage given by the equation: $Efficiency=\frac{UsefulEnergyOutput}{EnergyInput}\times 100\%$ $Efficiency=\frac{UsefulPowerOutput}{PowerInput}\times 100\%$

Momentum and Impulse:

Momentum is a vector quantity that is equal to the product of the mass and velocity of an object. This builds on a few laws of conservation and Newton’s second law of motion.

• Conservation of mass - due to the nature of chemical reactions, mass must be conserved A Lavoisier - 16th century
• Conservation of energy - The sum of all the energy in an isolated system is the same; energy is never created or destroy only changed in form G Leibniz - 16th century
• Conservation of momentum: Sina - 11th century/Descartes 15th century

$F=ma$ $F\Delta t=m\Delta v$ $\bar{p}=m\bar{v}$

Where $m$ is the mass $(kg)$, $v$ is the velocity $(m/s)$ and $p$ is the momentum in ($kgm/s$) (vector quantity)

Momentum in an isolated system is conserved, meaning that the sum of the initial momentum in an isolated system is also going to be equal to the sum of the final momenta within the same isolated system. $m_1{u}_1+m_2{u}_2=m_1{v}_1+m-2v_2$ p_{1i}+p_{2_i} = p_{1f}+p_{2f}$$$$ \Sigma \bar p_i=\Sigma \bar p_f Where the $i$ subscript is the initial velocity/impulse, $f$ subscript is the final velocity/impulse, $m$ is the mass of the object, $u$ is the initial velocity, $v$ is the final velocity, $p$ is the impulse

This concept applies in all dimensions; by breaking up the momentum into its components, the angles of new momenta can be ascertained.

Collisions

• Elastic collisions occur when kinetic energy of a collision is conserved. I.e. when objects collide they bounce back without deforming and there is no energy lost. (E.g. pool balls colliding/particles ‘bouncing off each other’); imagine a steel ball bounding on the floor
• Inelastic collisions occur when kinetic energy is not conserved. I.e. when objects collide but get deformed in the process; losing energy. (Say a volleyball hitting the floor) - They bounce back with a lower momentum to that of the initial momentum; imagine a ping pong ball landing on the floor. Relative to the ping-pong ball, this collision is more elastic.
• Perfectly inelastic collisions are collisions that lose all kinetic energy: imagine a lump of clay being dropped on the floor.

Explosions

Impulse

Impulse is a vector quantity equal to the change in momentum and the net force applied onto an object over a given time period. This can be represented mathematically as follows: $\Delta \bar{p}=m\Delta \bar{v}=\bar{F}\Delta t$

A common question is to have the area underneath a force vs. time graph represent the impulse. This can be used to determine the momentum and its component variables.

Newton’s Law of Gravitation

The gravitational force between two objects can be calculated using Newton’s universal law of gravitation. Generally:

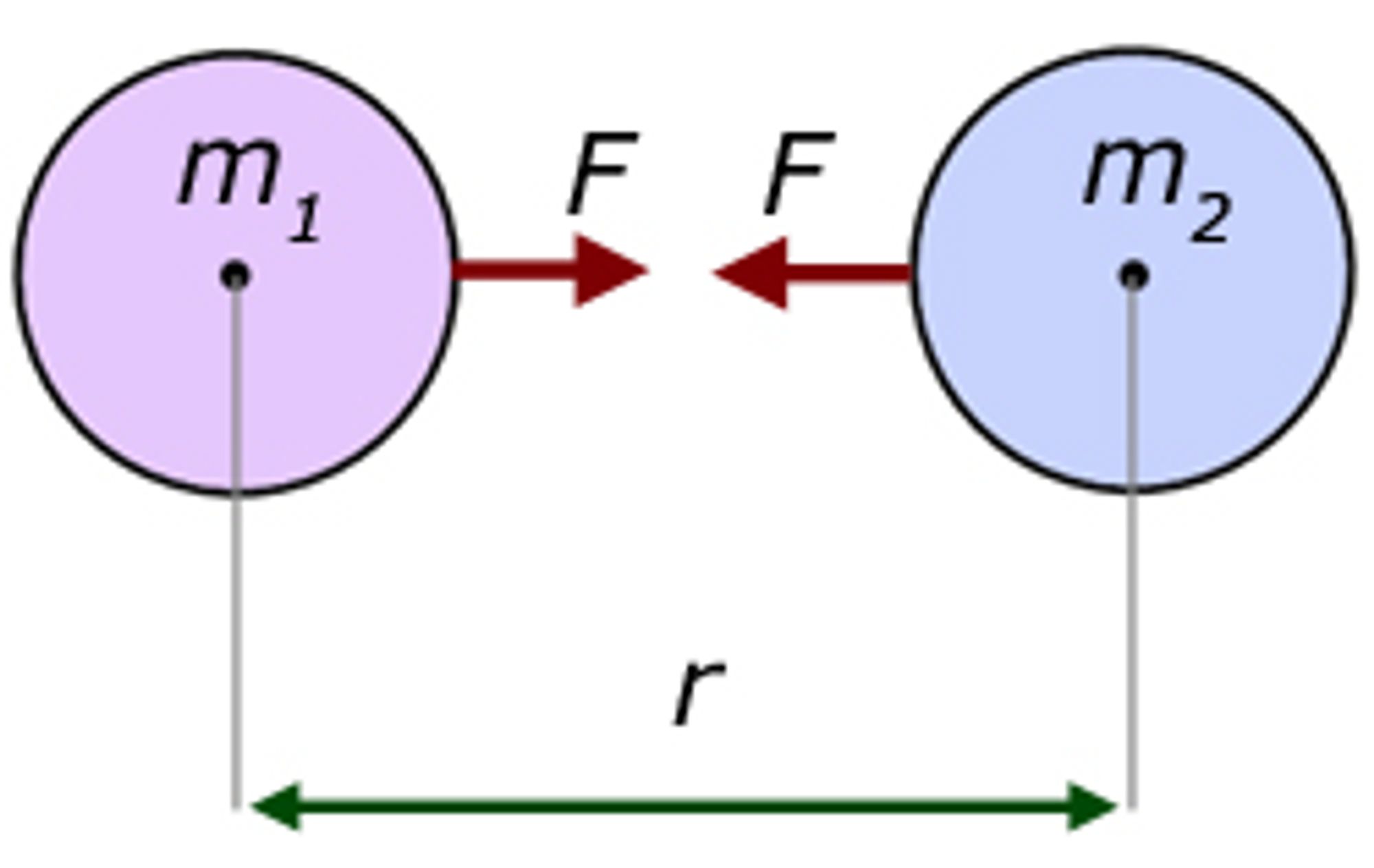
This can be described by the formula: $F_g=\frac{G{m}_1{m}_2}{R^2}$ Where $F_g$ is the gravitational force on an object (often weight), $G$ is the gravitational constant, $6.67430\times 10^{-11}\frac{N{m}^2}{k{g}^2}$, $m_1$ & $m_2$ are the masses of objects, and $R$ is the distance between two objects.

Condensing $G$, the mass of the Earth, $m_1(5.972\times 10^{24}kg)$ and the radius of the Earth, $R(6371km)$ accelerates a smaller object towards the earth at a rate of $\mathrm{9.81...}m/s^2$.

Gravitational Fields Strengths

The gravitational field strength at a point is the force per unit mass experienced by a test mass at that point. The gravitational field strength (g) due to an object is given by $g=\frac{F}{m}$ Where $g$ is the gravitational field strength, $F$ is the gravitational force, and $m$ is the mass of the object. Gravitational field strength at the surface of a planet

• The gravitational field strength at the surface of a planet can be calculated by using the equation for gravitational field strength and substituting M and r by the mass and the radius of the planet respectively.
• If we calculate the gravitational field strength at the surface of each using the mass and the radius of the Earth, we would obtain the value 9.81m/s^2, which is equal to the acceleration due to gravity on the surface of the Earth.
• Different planets have different radii and masses. Consequently, different planets have different gravitational field strengths.

Air Resistance

It is only because of air resistance that objects of similar weight fall at different rates.

Circular Motion

Period, Frequency, Angular Displacement, and Angular Velocity

Uniform circular motion refers to circular motion at constant speed. In a uniform circular motion, speed is constant while (angular) velocity and (angular) acceleration are constantly changing.

• While the magnitude of its velocity remains constant, the direction of its velocity is constantly changing.
• The acceleration causing this change in velocity is always directed towards the center of the circular path.

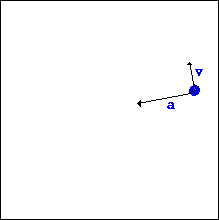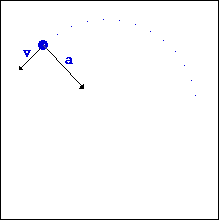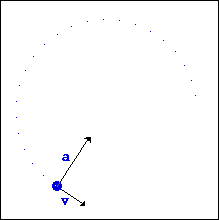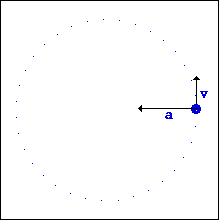
The period is the time taken for the object to complete one full circle and is usually calculated in seconds. The frequency can be calculated by 1/period and is usually measured in Hz.

Centripetal Force

Centripetal force is the corresponding force (resultant force) which causes the centripetal acceleration. Properties:

• Direction: Pointing towards the center of the circle / perpendicular to the instantaneous velocity
• Magnitude: $\Sigma F=\frac{m{v}^2}{r}$
• Work done by centripetal force = 0
• Centripetal force is ; rather, it is just the name we give to the  causing a circular motion. (not a type of force net force).

Centripetal Acceleration

The acceleration which gives rise to a circular motion is called the centripetal acceleration. Its magnitude is given by: $a={\omega }^{2}r=\frac{v^2}{r}$ Where $a$ is acceleration, $\omega$ is angular velocity, $v$ is scalar velocity, $r$ is radius. It is directed towards the center of the circular motion and is perpendicular to the instantaneous velocity of the object.

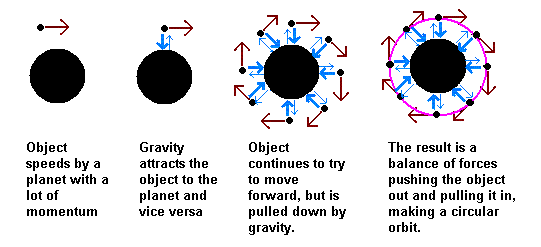
Gravitational Circular Motion

Energy Changes

In a SHM, there is an interchange between KE and PE throughout the motion. However, the total energy remains constant.

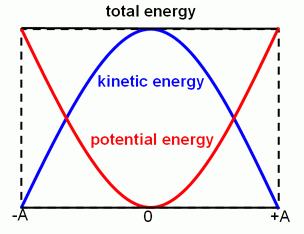
• At maximum displacement, PE is at max while KE=0
• At zero displacement, KE is at max while PE=0
• At minimum displacement, PE is at max while KE=0
• Total energy (KE+PE) remains constant throughout the motion $E_m=K_{tr}+U_{elas}=\frac{1}{2}m{v}^2+\frac{1}{2}k{x}^2$ Where $E_m$ is the mechanical (total) energy of a system, $K_{tr}$ is the kinetic energy of the object, $U_{elas}$ is the (elastic) potential of the object, $v$ is the scalar speed of the object, $m$ is the mass of the object, $k$ is the spring constant, and $x$ is the extension (or compression) away (or towards) the equilibrium state.