Mechanical equilibrium

2024-10-0411:05 Status:PHYS106 Tags:

Mechanical equilibrium occurs when velocities are zero and forces add to zero for each part of a physical system. Or $\Sigma \vec{F}=0$

Restoring Forces:

For a (stable) equilibrium configuration, a displacement in one direction leads to a net force in the other direction.

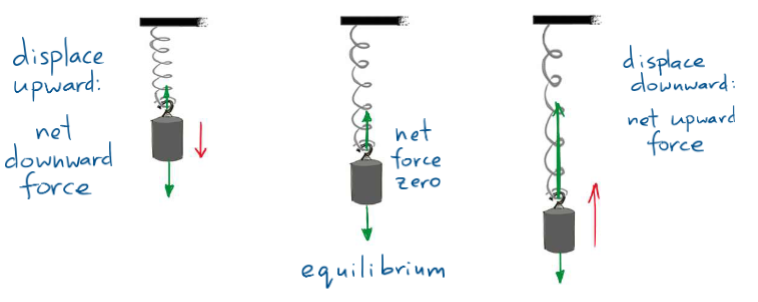
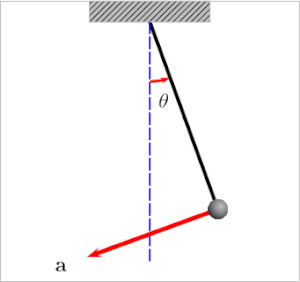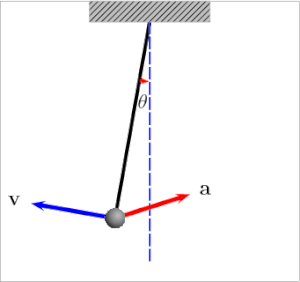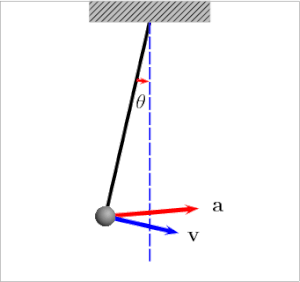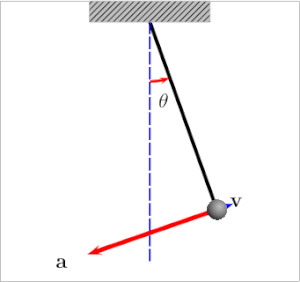
Oscillations

The restoring forces decay to 0 as an object comes to the equilibrium position. For instance, when a book is placed on a table, it makes a sound - this is the result of several oscillations happening within a fraction of a second.

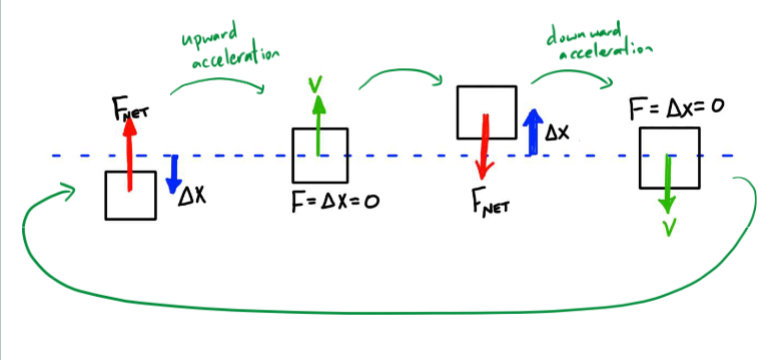
Net Force vs. Displacement Graph + Hooke’s Law

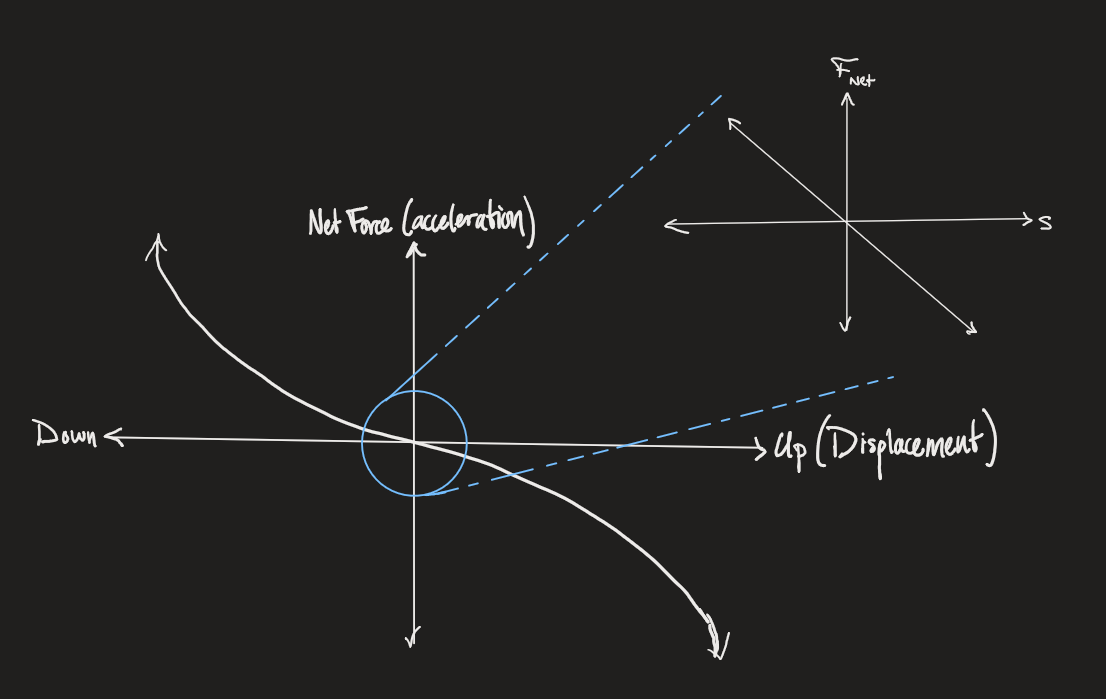Where the zoomed in version approaches a linear approximation for which Hooke’s Law applies.

Hooke’s Law: Applies to almost any system perturbed a small amount from its stable equilibrium: $F_{restoring}=-kx$ Where $k$ is a “spring/restoring” constant and $x$ is displacement.

This is exact for an ideal spring.

Oscillations with Hooke’s Law

Newton found: $a=\frac{F}{m}=-\frac{k}{m}\cdot x=\frac{dv}{dt}=-\frac{k}{m}\cdot x=\frac{dx}{dt}=v$
Thus we can find how velocity and position change with time. The solution is:

x(t) = A\cos (\omega t + \phi), \ \ \ \ \omega = \sqrt\frac k m \\ \frac {dx} {dt} = v(t) =-Asin (\omega t)\cdot \omega \\ \frac {dv} {dt} = a(t) = -A\omega ^2 \cos (\omega t) \end{gather}$$ Where $A$ is the amplitude of the wave (max displacement from equilibrium); $\omega$ is $\sqrt \frac k m$ and affects the horizontal stretch, thus the period and consequently, the frequency of the wave; $\phi$ is the phase shift (where the system is displaced from). However, we want: $$-\frac k m A \cos (\omega t), \ \ \ \ \omega = \sqrt \frac k m $$ ![[Pasted image 20241004115048.png]]